In a groundbreaking mathematical breakthrough, researchers have finally solved a 380-year-old geometry problem left unfinished by the renowned philosopher and mathematician René Descartes. This discovery sheds new light on classical geometry and has implications for modern mathematical research.
The Problem Left Unfinished by Descartes
René Descartes, best known for his contributions to philosophy and analytical geometry, proposed a complex geometric problem in 1644 in his work La Géométrie. While he laid the foundation for modern coordinate geometry, one specific problem related to circle packing and curvature calculations remained unresolved.
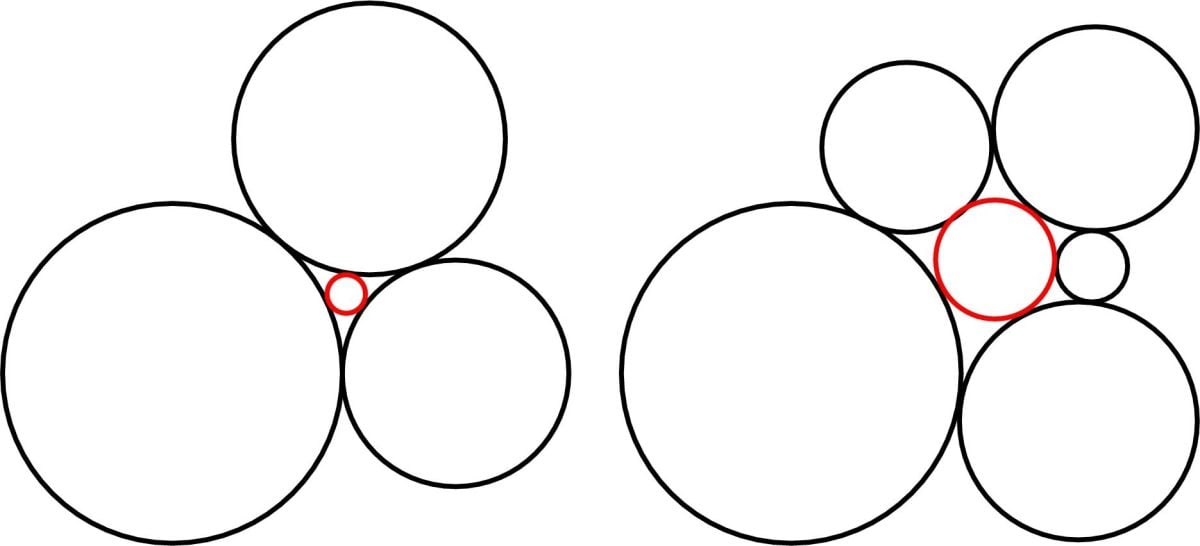
Descartes introduced an equation, now known as the Descartes Circle Theorem, which determines the relationship between four mutually tangent circles. However, a generalization of this theorem involving three-dimensional spheres and higher-dimensional spaces had remained an unsolved challenge—until now.
How Mathematicians Cracked the 380-Year-Old Puzzle
A team of mathematicians, using modern computational techniques and advanced algebraic geometry, has extended Descartes’ theorem beyond two-dimensional circles to include higher-dimensional analogs. By employing computational algorithms and machine learning models, they uncovered patterns that had eluded generations of mathematicians.
Their research successfully established a formula that describes the curvature relationships of spheres in three-dimensional space and even extends into four or more dimensions. This achievement not only completes Descartes’ original work but also opens doors to further discoveries in geometry, physics, and even cosmology.
Implications of the Discovery
This mathematical breakthrough has far-reaching consequences:
Geometry and Topology: The findings enhance our understanding of curvature in complex spaces, aiding research in topology and higher-dimensional geometry.
Physics and Cosmology: The study of sphere packing and curvature relationships plays a role in general relativity and the modeling of gravitational fields.
Computer Science and Engineering: Advanced algorithms derived from this theorem could improve computer graphics, structural engineering, and even optimization problems in artificial intelligence.
What’s Next in Geometry?
The solution to Descartes’ unfinished problem paves the way for deeper exploration into higher-dimensional mathematics. Researchers are already investigating its applications in quantum physics, network theory, and artificial intelligence.
This historic breakthrough is a testament to the enduring power of mathematical curiosity and perseverance. The resolution of a centuries-old problem left by Descartes not only honors his legacy but also inspires future generations to continue exploring the mysteries of mathematics.













+ There are no comments
Add yours